水族館や海中映像などでイワシが群れをなして泳いでいる様子を眺めたことがある人は多いと思います。イワシは群れを作ることで天敵を混乱させ、群れとして生存する確率を上げていると言われています。同様に、ムクドリやスズメなどの鳥も群れを作ることで、タカなどの外敵から身を守っています。
このように、"群れる"行動は生物で一般的に見られる集団行動です。今回は、群れの現象を計算機上で再現したVicsekモデルというシミュレーションモデルを紹介いたします。
Vicsekモデルシミュレーション
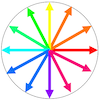
魚の群れの動きを再現したシミュレーション(色は進行方向を示す)

Vicsekモデルとは?
上の動画では、魚に見立てた1万本の棒が泳いでおり、魚の群れに似た独特の動きを再現しています(群れの違いを見やすくするため、進む角度によって色を変えて表示しています)。
Vicsekモデルとは、集団運動をモデル化して計算機上で再現したハンガリーの科学者Tamas Vicsek(1995)から名付けられています。一本一本の棒はそれぞれ自立して運動していますが、周囲の棒たちと協調した向きに動こうとすることで群れが生じます。
このように生物の動きを模したVicsekモデルは、モデルが少しずつ修正されながら、近年のドローン群の自動運転に関する研究や、混雑した駅や交差点での人の動きの予測、農業被害を起こすイナゴの大群の予測、がん細胞の集団移動のメカニズム、ナノサイズの物質の集団的な挙動制御によるナノデバイスの開発など多岐の分野で研究されています。
プログラミングの方法
Vicsekモデルでは, 次式のように棒それぞれが計算ステップ毎に, 一定速度\(v_{0}\)で方向\(s=(cos\theta, sin\theta)\)に進んでいます. \begin{equation} r_{i}^{t+\Delta t}=r_{i}^{t}+\Delta t\ v_{0}\ s_{i}^{t} \end{equation} ここで, 進む方向については次式のように, ある番号\(\ i\ \)番の棒に着目すると, 一歩進む毎に下の図のように, 棒\(\ i\ \)から距離\(\ r_{cut}\ \)と視野角\(\ \theta_{cut}\ \)の範囲に存在する周囲の\(\ j\ \)番目の棒の進む方向をすべて合わせた平均を計算して, その方向にゆらぎ\(\ \eta\ \xi_{i}^{t}\ \)を加えた方向\(\ \theta_{i}^{t+\Delta t}\ \)へと進んでいきます(ここで, \(\ \eta\ \)は定数, \(\ \xi\ \)は-0.5から0.5までの乱数で, \(\ \eta\ \)が大きいほど, 動く方向がノイズの影響を受けるようになっています. \(\ n_{ij}^{t}\ \)は, 棒\(\ i\ \)から距離\(\ r_{cut}\ \)と視野角\(\ \theta_{cut}\ \)の範囲で1となり, それ以外の領域でゼロになる関数, \( m_{i}\ \)は, 棒\(\ i\ \)周囲に存在している棒\(\ j\ \)の個数です).\begin{equation} \theta_{i}^{t+\Delta t} = Arg \left[\sum_{j}{n_{ij}^{t}s_{j}^{t}} +m_{i}\ \eta\ \xi_{i}^{t} \right] \end{equation}
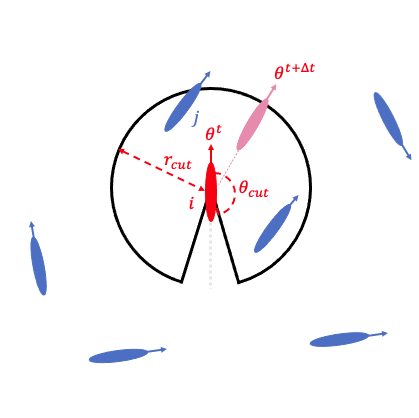
上の図のように, 棒は後方の視野に限界があり, 前にいる棒の動きに従って動いているのですが, 群れの先頭にいる棒の進行方向には自由があるため, 先頭の棒が少し方向転換しただけでその動きが群れ全体に伝わっていき, 大きな方向転換が起こることになります. その結果, 予測できない方向に群れが進んでいきます.
下には, 少し規模を大きくした実験をお見せします.
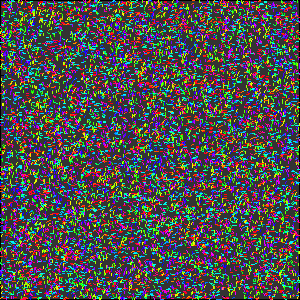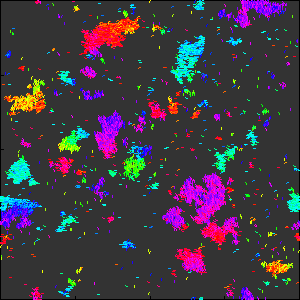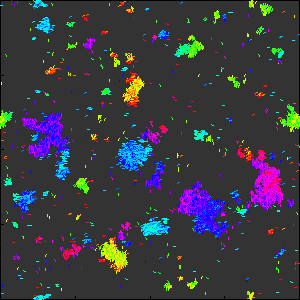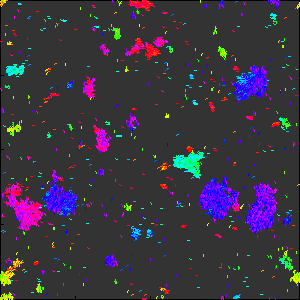
統計物理におけるVicsekモデル
Vicsekモデルでは, 乱数の影響度\(\ \eta\ \)の値をゼロから徐々に大きくしていくと, ある値から群れの動きを取らないほどノイズが大きくなり, 最終的にバラバラの状態になることが予想されます. このように, 系の秩序が大きく変化することを相転移と言い, 統計物理学では, 例えば固体-液体-気体の三相や非磁性体-磁性体の相変化など大きなトピックの一つとして扱われています.それでは, 実際に\(\ \eta\ \)を動かして相転移を起こしてみましょう. ここで, 全体の秩序を測定するためのパラメーターSを以下のように定義します \begin{equation} S=\frac{1}{N}|\sum_{j=1}^{N} s_{i}^{t}| \end{equation} すべての棒の進行方向が同じ方向のとき, S=1.0となります. 以下, 棒の本数2500本, サイズ50*50, 密度1.0, 視野角\(\ \theta_{cut}\ \)=0.8\(\ \pi\ \), 距離\(\ r_{cut}\ \)=1.0, v0=1.0の条件で, \(\ \eta\ \)=2.0から2.7まで変化させたとき秩序パラメータSの時間的推移を80万ステップ計算します.
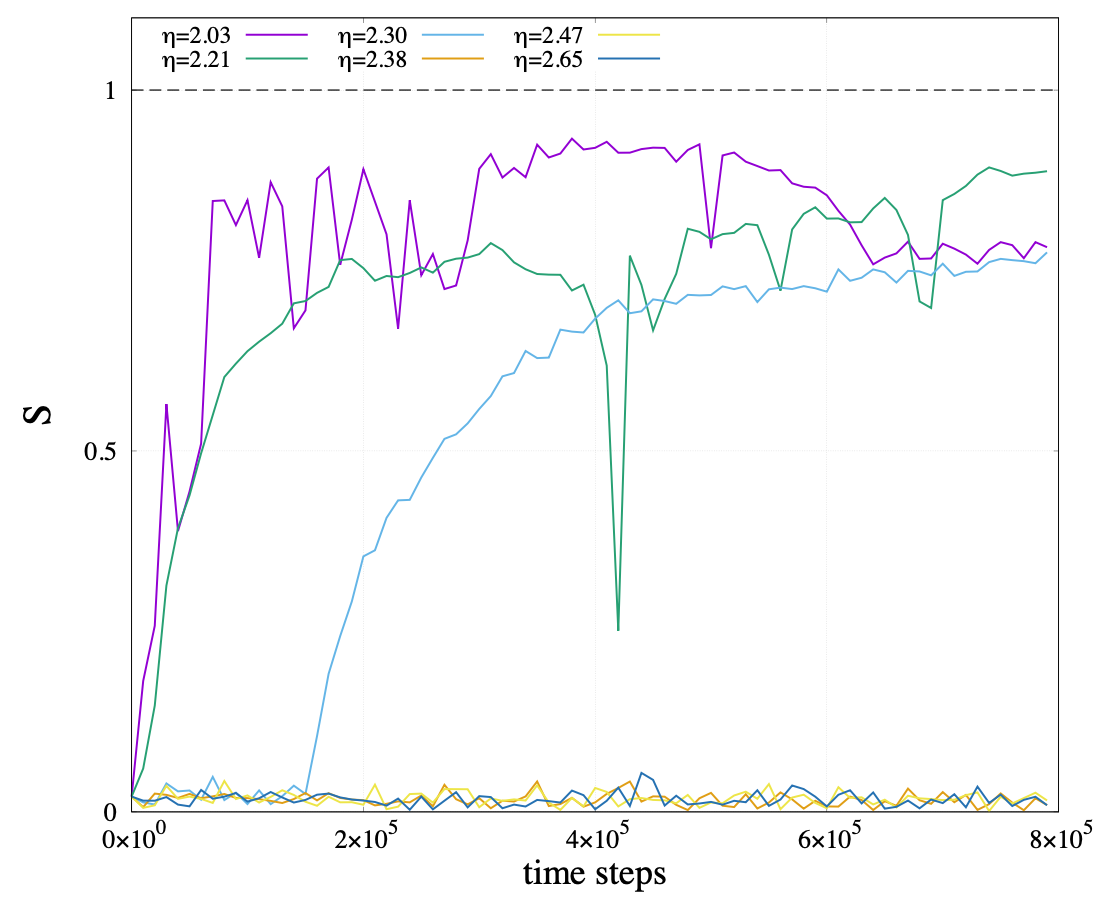
上の図から, 秩序変数がある程度一定になる60万ステップから80万ステップまでのSの平均値を\(\ \eta\ \)の値ごとに計算すると, 以下のような図が得られます.
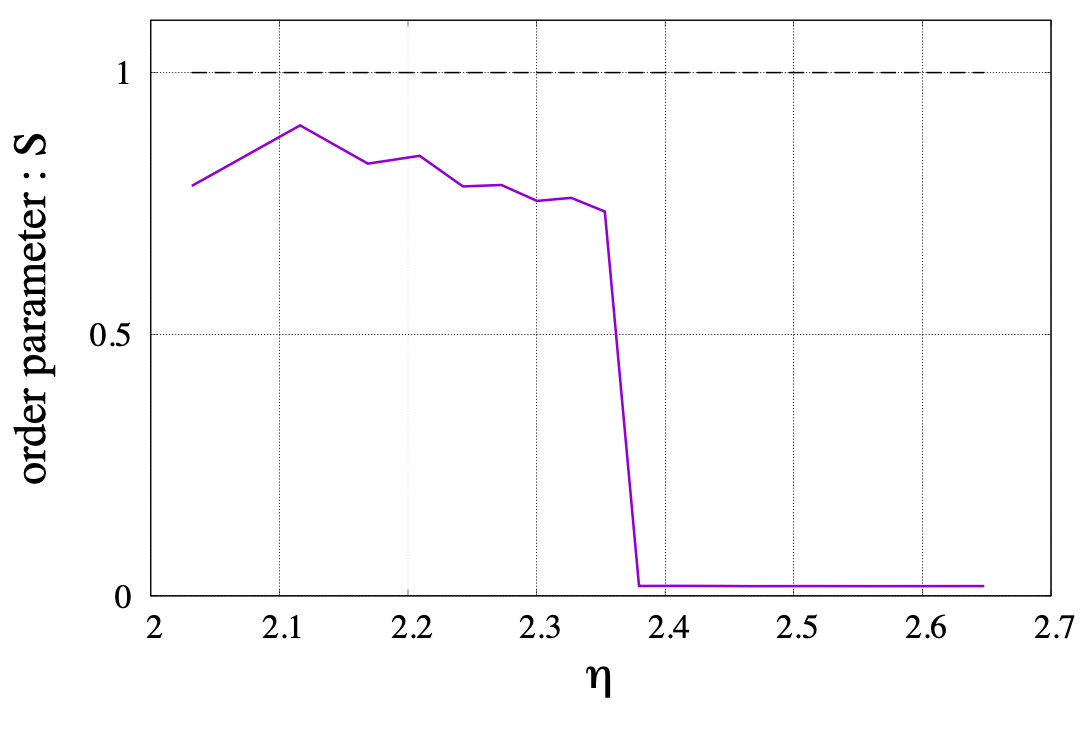
上の図から、先ほど述べたとおりηの値が大きくなるほど秩序さが失われ、系が乱雑になっていくことが分かります。また、秩序変数Sがη=2.365付近で急激に変わることが分かります。このように、系を転移させることができました。また、そのような転移点において、Vicsek waveという平面波が生じるなどカオス的な現象が現れることが知られています。